Revisiting k-nearest neighbor benchmarks in self-supervised learning
Published:
Self-Supervised Learning and KNN benchmarks
Deep learning has advanced performance in several machine learning problems throught the use of large labeled datasets. However, labels are expensive to collect and at times leads to biases in the trained model arising from the labeling of the data. One technique, that has gained interest in recent years, to solve these issues is self supervised learning (Self-SL). The goal of self-SL is to learn representations from data using the data itself as supervision (leveraging inductive biases that we assume on the system) i.e., a model is trained to produce representation such that the extracted features perform well on a artificially generated task for which ground truth is available.
How does one quantify the representations obtained? Standard protocols for benchmarking self-SL models involve using a linear or weighted k-nearest neighbor classification (KNN) on features extracted from the learned model whose parameters are not updated.However, both these evaluations are sensitive to hyperparameters making the evaluation and comparison complicated. For e.g., in linear evaluations, one often applies selected augmentations to the input to train the linear classifier on top of the feature extractor in addition to hyperparameters used for training the classifier. A weighted k-nearest neighbor classifier, on the other hand, avoids data augmentations but still suffers from the selection of hyperparameter k. One observes large variance in accuracy in both these evaluation frameworks based on the hyperparameter/augmentations chosen making the comparison of feature extractors obscure. Ideally, one would want an evaluation protocol that does not require augmentations or hyperparameter tuning and can be run quickly given the features of the data. In this post, I hope to convince you with an alternate neighborhood based classifier that can satisfy these requirements exactly. In fact, we will see that not only is the proposed classifier robust but is also capable of performing better if not at par than the previous evaluation methods in terms of classification accuracy.
Non Negative Kernel regression (NNK)
In NNK, neighborhood selection is formulated as a signal representation problem, where each data point is to be approximated using a dictionary formed by its neighbors. This problem formulation, for each data point, leads to an adaptive and principled approach to the choice of neighbors and their weights. While KNN is used as an initialization, NNK performs an optimization akin to orthogonal matching pursuit in kernel space resulting in a robust representation with a geometric interpretation. Geometrically, KRI reduces to a series of hyper plane conditions, one per NNK neighbor, which applied inductively lead to a convex polytope around each data point as show in Fig. below. In words, NNK ignores neighbors that are further away along a similar direction as an already chosen point and looks for neighbors in an orthogonal or different direction.
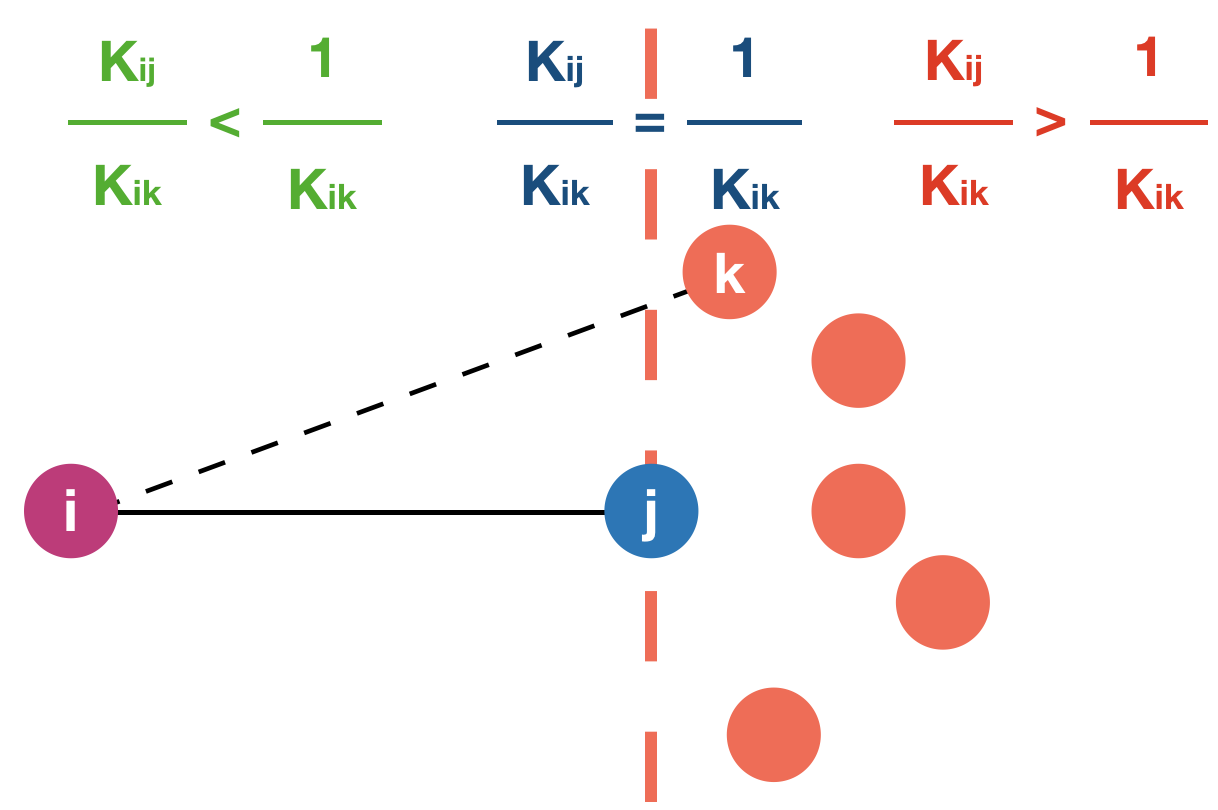
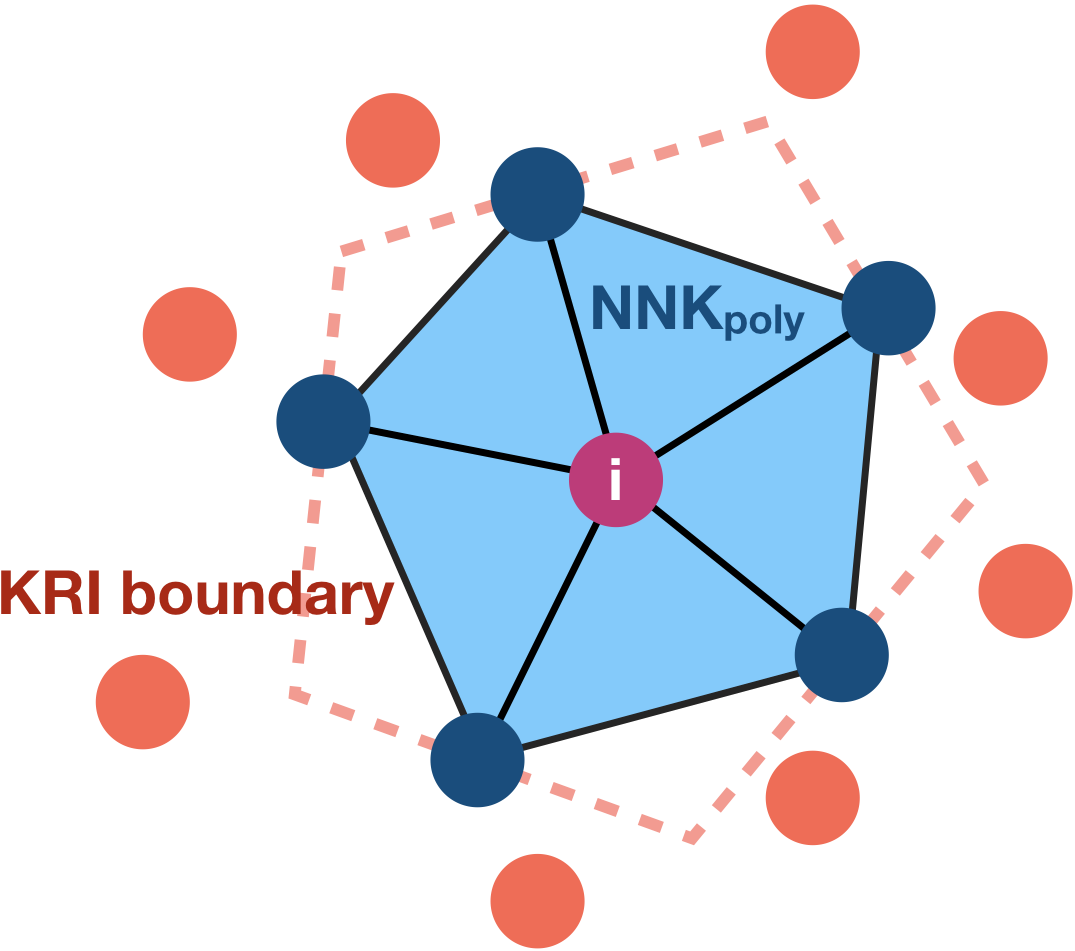
Left: KRI plane (dashed orange line) corresponding to chosen neighbor `j`. Data points to the right of this plane will be not be selected by NNK as neighbors of `i`. Right KRI boundary obtained by inductive application of KRI plane and associated convex polytope formed by NNK neighbors at `i`.
Note that, this perspective provides an alternative to the conventional thinking of local neighborhoods as hyperspheres or balls of certain radius in space. This is made possible in NNK, by taking into account the relative positions of nodes j and k using the metric on (j,k), in addition to the metric on (i,j) and (i,k) that were previously used for the selection and weighing of neighbors j,k to node i.
Application of NNK for classification is further interesting from a recent theoretical point of view: interpolative classifiers, namely classifiers with training error 0, are capable of generalizing well to test data contrary to the conventional wisdom (interpolation ⇒ poor generalization). Note that overparameterized neural network models today are increasingly trained to zero training error and can be considered to fall under this category of interpolative classifiers. In the experiments that follow, we will use a normalized cosine kernel (cosine kernel shifted and scaled to have values between 0 and 1) for NNK and KNN.
Self-SL evaluation with NNK
Table below lists Top-1 Linear, weighted KNN and NNK classification accuracy on ImageNet using a fixed bacbone architecture ResNet-50 that was trained using different self-SL training strategies. The evaluation protocol follows a standard setup where one evaluated performance on validation dataset based on labeled training dataset. The KNN and NNK evaluations were done using a self-SL framework VISSL with officially released model weights and setting the parameter k, number of neighbors, to 50. The results listed for linear evaluations are as reported on the corresponding self-SL papers and was not validated by us.
| Method | Linear | KNN | NNK |
|---|---|---|---|
| Supervised | 76.1 | 74.5 | 75.4 |
| MoCo-v2 | 71.1 | 60.3 | 64.9 |
| DeepClusterV2 | 75.2 | 65.8 | 70.7 |
| SwAV | 75.3 | 63.2 | 68.7 |
| DINO | 75.3 | 65.6 | 71.1 |
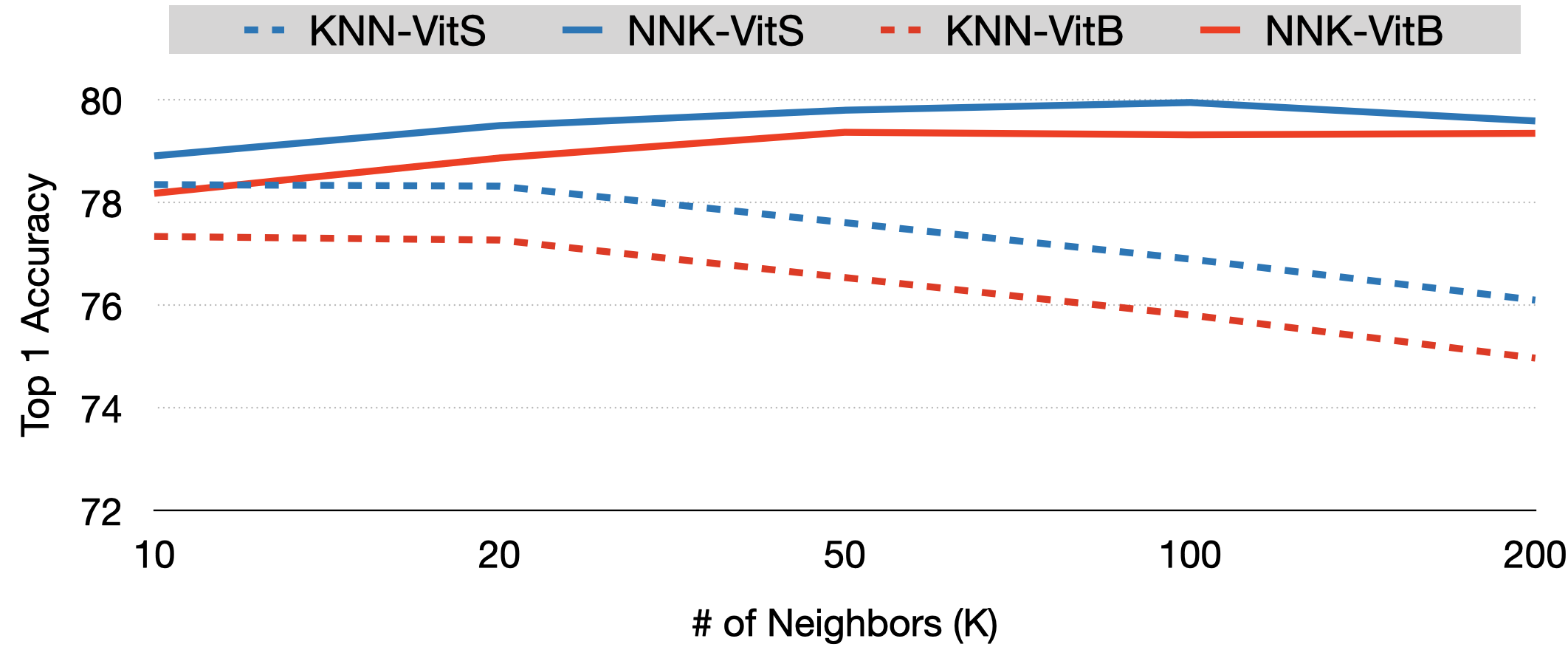
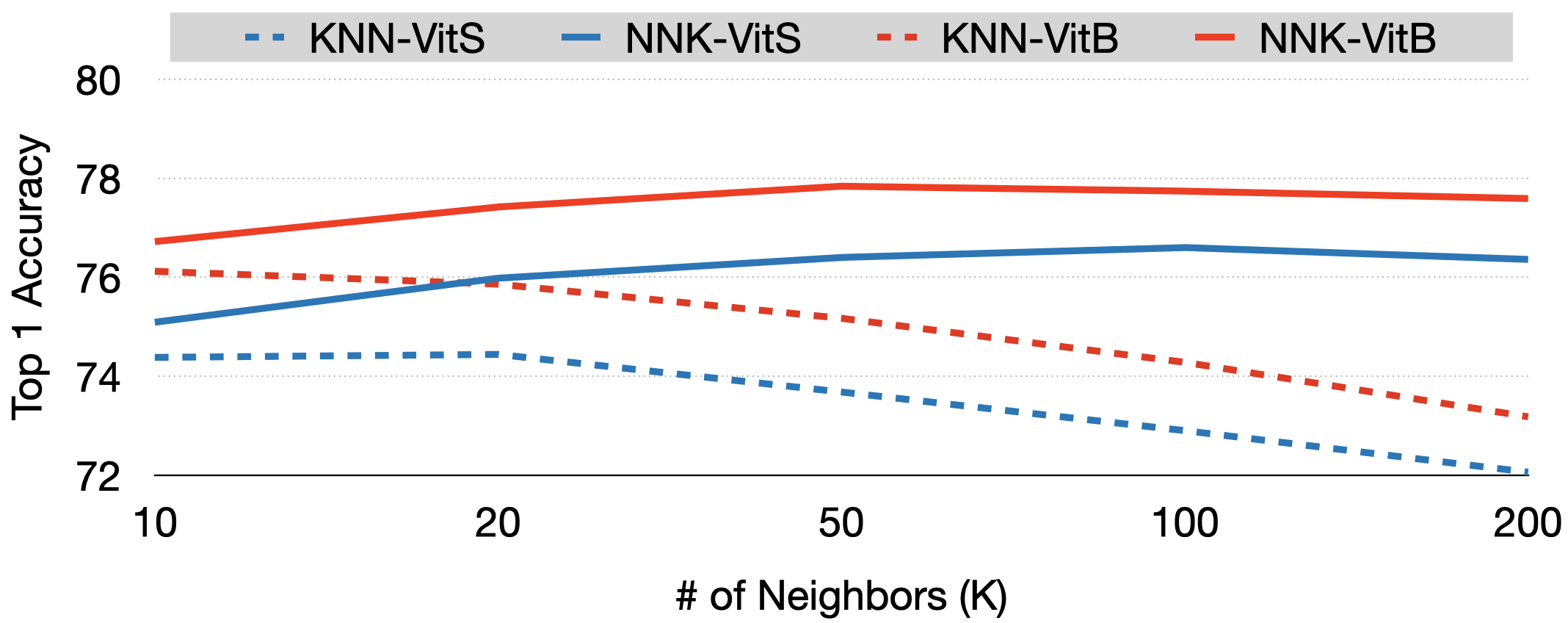
To evaluate the robustness of NNK relative to KNN we will use a recently introduced self-SL model, DINO (distillation with no labels), as our baseline model and compare Top-1 accuracy on ImageNet for different values of k. As can be seen in Figure below, NNK not only consitently outperforms a weighted KNN classifer but does so in a robust manner. Further, unlike the KNN whose performance decreases as k increases, NNK improves with k. This can be explained by the fact that NNK accommodates new neighbors only if they belong to a new direction in space that improves its interpolation whereas a KNN simply interpolates with all k neighbors. NNK classifier in this setup achieves performance on par if not better than the linear classifier model with the small ViT model achieving ImageNet top-1 accuracy of 79.8%, the best performance by a non parametric classifier in conjunction with self-SL models.
Discussion
Several machine learning methods leverage the idea of local neighborhood by using methods such as KNN, ∈-neighborhood to better design and evaluate pattern recognition models. However, the choice of parameters such as k is often made experimentally, e.g., via cross-validation, leading to local neighborhoods without a clear interpretation. NNK formulation allows us to overcome this shortcomings resulting in a superior framework that is adaptive to the local distribution of samples. As show in this post and our related works, NNK does exhibit robust and superior performance relative to standard local methods. Ultimately, our goal is for the NNK framework to encourage and revisit the use of interpretable and robust neighborhood methods in machine learning - for e.g., consider the problem of model distillation or clustering where NNK could be used to enforce better local consistency regularization.
Source code for experiments in this post are available at github.com/shekkizh/VISSL_NNK_Benchmark
